This "dents" the likelihood surface by reflecting points better than a threshold back across the threshold (think of taking a hollow plastic model of a mountain and punching the top so it's a volcano). It then uses essentially a Metropolis-Hastings walk to wander around the new rim. It adjusts the proposal width so that it samples points around the desired likelihood. This is better than using the curvature at the maximum likelihood estimate since it can actually sample points in case the assumptions of the curvature method do not hold. It is better than varying one parameter at a time while holding others constant because that could miss ridges: if I am fitting 5=x+y, and get a point estimate of (3,2), the reality is that there are an infinite range of values of x and y that will sum to 5, but if I hold x constant it looks like y is estimated very precisely. Of course, one could just fully embrace the Metropolis-Hastings lifestyle and use a full Bayesian approach.
dent_walk(
par,
fn,
best_neglnL,
confidence_level = 0.95,
delta = NULL,
nsteps = 1000,
print_freq = 50,
lower_bound = 0,
upper_bound = Inf,
adjust_width_interval = 100,
badval = 1e+09,
sd_vector = NULL,
debug = FALSE,
restart_after = 50,
quiet = TRUE,
sphere_probability = 0,
...
)Arguments
- par
Starting parameter vector, generally at the optimum. If named, the vector names are used to label output parameters.
- fn
The likelihood function, assumed to return negative log likelihoods
- best_neglnL
The negative log likelihood at the optimum; other values will be greater than this.
- confidence_level
The confidence level represents the long-run proportion of CIs (at the given confidence level) that theoretically contain the true value of the parameter. For example, out of all intervals computed at the 95% level, 95% of them should contain the parameter's true value
- delta
How far from the optimal negative log likelihood to focus samples
- nsteps
How many steps to take in the analysis
- print_freq
Output progress every print_freq steps.
- lower_bound
Minimum parameter values to try. One for all or a vector of the length of par.
- upper_bound
Maximum parameter values to try. One for all or a vector of the length of par.
- adjust_width_interval
When to try automatically adjusting proposal widths
- badval
Bad negative log likelihood to return if a non-finite likelihood is returned
- sd_vector
Vector of the standard deviations to use for proposals. Generated automatically if NULL
- debug
If TRUE, prints out much more information during a run
- restart_after
Sometimes the search can get stuck outside the good region but still accept moves. After this many steps without being inside the good region, restart from one of the past good points
- quiet
If TRUE, will quiet the likelihood function outputs
- ...
Other arguments to fn.
Value
A dentist object containing results, the data.frame of negative log likelihoods and the parameters associated with them; acceptances, the vector of whether a proposed move was accepted each step; best_neglnL, the best value passed into the analysis; delta, the desired offset; all_ranges, a summary of the results.
Details
While running, it will display the current range of likelihoods in the desired range (by default, the best negative log likelihood + 2 negative log likelihood units) and the parameter values falling in that range. If things are working well, the range of values will stabilize during a search.
The algorithm tunes: if it is moving too far away from the desired likelihoods, it will decrease the proposal width; if it staying in areas better than the desired likelihood, it will increase the proposal width. It will also expand the proposal width for parameters where the extreme values still appear good enough to try to find out the full range for these values.
In general, the idea of this is not to give you a pleasingly narrow range of possible values -- it is to try to find the actual uncertainty, including finding any ridges that would not be seen in univariate space.
Examples
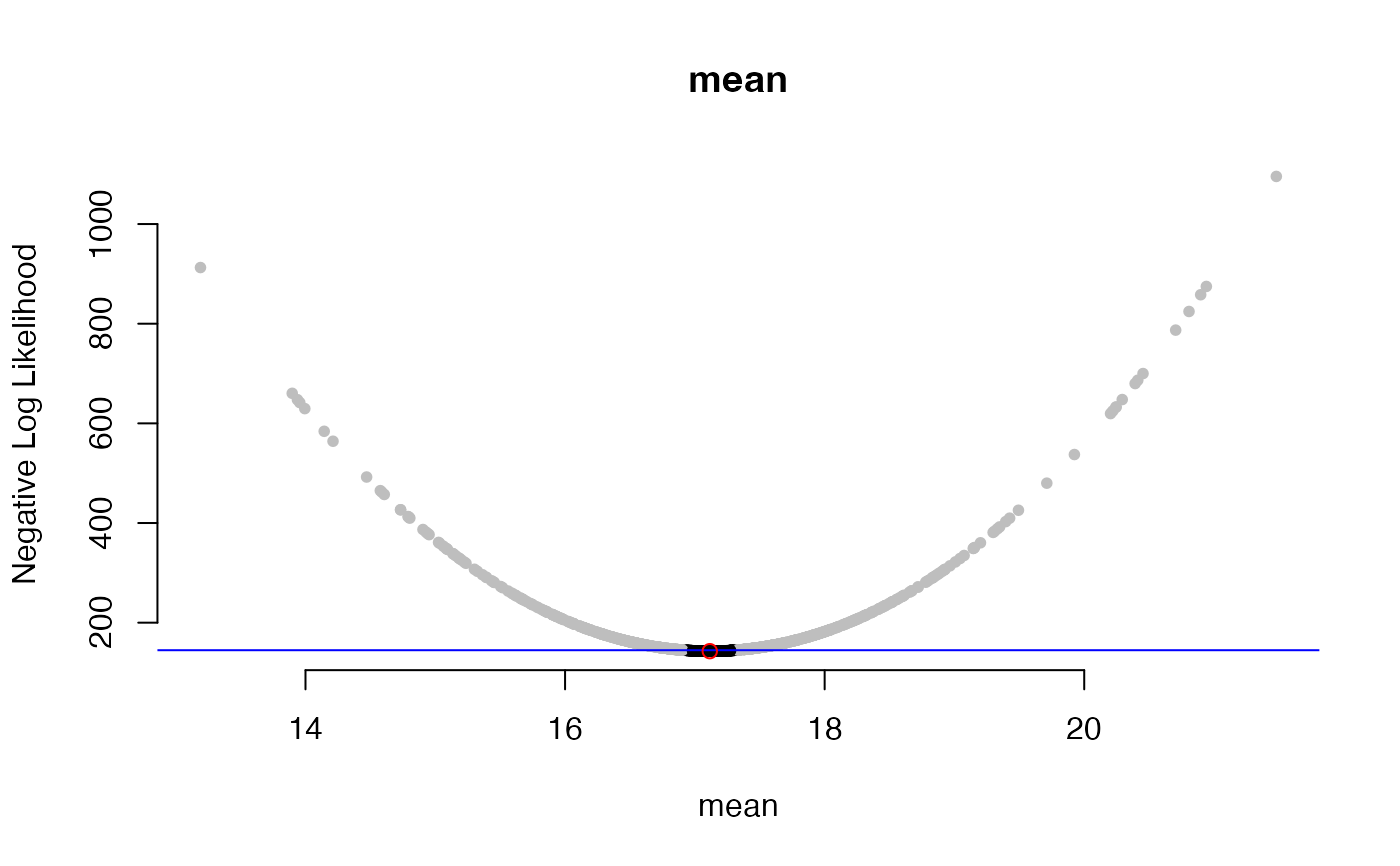
# Univariate case
sims <- stats::rnorm(100, mean=17)
possible_means <- seq(from=16, to=18, length.out=100) # for optimize
# Make sure we have a function that takes in a parameters vector, other arguments if needed,
# and returns the negative log likelihood
dnorm_to_run <- function(par, sims) {
return(-sum(stats::dnorm(x=sims, mean=par, log=TRUE)))
}
optimized_results <- stats::optimize(dnorm_to_run,interval=range(possible_means),
sims=sims, maximum=FALSE)
best_par <- optimized_results$minimum
names(best_par) <- "mean"
best_neglnL <- optimized_results$objective
dented_results <- dent_walk(par=best_par, fn=dnorm_to_run, best_neglnL=best_neglnL, sims=sims)
#> [1] "Calculating intervals at a confidence level of 95%"
#> [1] "Done replicate 50"
#> [1] "CI of values (the 5 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 17.00198
#> [2,] 143.9305 17.26405
#> [1] "Rough volume of good region is 0.262070598535072"
#> [1] "Done replicate 100"
#> [1] "CI of values (the 8 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 17.00198
#> [2,] 143.9305 17.26405
#> [1] "Rough volume of good region is 0.262070598535072"
#> [1] "Done replicate 150"
#> [1] "CI of values (the 11 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 16.96477
#> [2,] 143.9438 17.26405
#> [1] "Rough volume of good region is 0.299280440285546"
#> [1] "Done replicate 200"
#> [1] "CI of values (the 17 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 16.95192
#> [2,] 144.1450 17.26405
#> [1] "Rough volume of good region is 0.312136899864679"
#> [1] "Done replicate 250"
#> [1] "CI of values (the 22 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 16.95192
#> [2,] 144.1450 17.27379
#> [1] "Rough volume of good region is 0.321876371896654"
#> [1] "Done replicate 300"
#> [1] "CI of values (the 25 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 16.95192
#> [2,] 144.5872 17.30299
#> [1] "Rough volume of good region is 0.351070303996405"
#> [1] "Done replicate 350"
#> [1] "CI of values (the 29 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 16.94866
#> [2,] 144.5872 17.30299
#> [1] "Rough volume of good region is 0.354327637837219"
#> [1] "Done replicate 400"
#> [1] "CI of values (the 38 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 16.92518
#> [2,] 144.6165 17.30299
#> [1] "Rough volume of good region is 0.377810801319285"
#> [1] "Done replicate 450"
#> [1] "CI of values (the 43 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 16.92518
#> [2,] 144.6508 17.30634
#> [1] "Rough volume of good region is 0.381161305913135"
#> [1] "Done replicate 500"
#> [1] "CI of values (the 55 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 16.92518
#> [2,] 144.6508 17.30634
#> [1] "Rough volume of good region is 0.381161305913135"
#> [1] "Done replicate 550"
#> [1] "CI of values (the 67 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 16.92518
#> [2,] 144.6508 17.30634
#> [1] "Rough volume of good region is 0.381161305913135"
#> [1] "Done replicate 600"
#> [1] "CI of values (the 78 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 16.92518
#> [2,] 144.6508 17.30634
#> [1] "Rough volume of good region is 0.381161305913135"
#> [1] "Done replicate 650"
#> [1] "CI of values (the 88 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 16.92518
#> [2,] 144.6508 17.30634
#> [1] "Rough volume of good region is 0.381161305913135"
#> [1] "Done replicate 700"
#> [1] "CI of values (the 101 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 16.92518
#> [2,] 144.6508 17.30634
#> [1] "Rough volume of good region is 0.381161305913135"
#> [1] "Done replicate 750"
#> [1] "CI of values (the 116 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 16.92518
#> [2,] 144.6508 17.30634
#> [1] "Rough volume of good region is 0.381161305913135"
#> [1] "Done replicate 800"
#> [1] "CI of values (the 132 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 16.92518
#> [2,] 144.6508 17.30634
#> [1] "Rough volume of good region is 0.381161305913135"
#> [1] "Done replicate 850"
#> [1] "CI of values (the 148 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 16.92518
#> [2,] 144.6508 17.30634
#> [1] "Rough volume of good region is 0.381161305913135"
#> [1] "Done replicate 900"
#> [1] "CI of values (the 164 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 16.92518
#> [2,] 144.6508 17.30634
#> [1] "Rough volume of good region is 0.381161305913135"
#> [1] "Done replicate 950"
#> [1] "CI of values (the 181 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 16.92518
#> [2,] 144.6508 17.30634
#> [1] "Rough volume of good region is 0.381161305913135"
#> [1] "Done replicate 1000"
#> [1] "CI of values (the 195 replicates within 1.92072941034706 neglnL of the optimum)"
#> neglnL mean
#> [1,] 142.8176 16.92518
#> [2,] 144.6508 17.30634
#> [1] "Rough volume of good region is 0.381161305913135"
plot(dented_results)
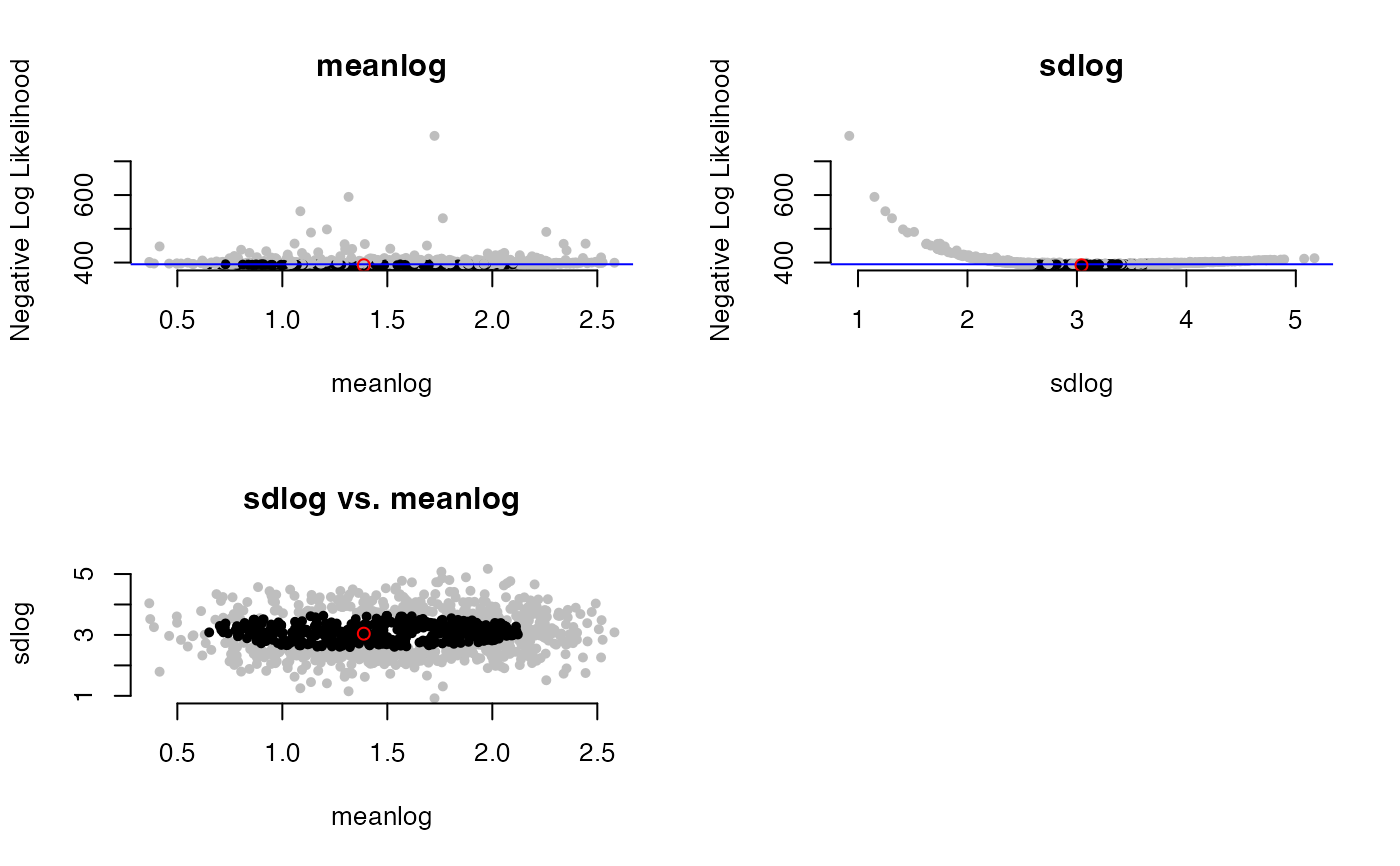
 # Multivariate case
sims <- stats::rlnorm(100, meanlog=1, sdlog=3)
dlnorm_to_run <- function(par, sims) {
return(-sum(stats::dlnorm(sims, meanlog=par[1], sdlog=par[2], log=TRUE)))
}
optimized_results <- stats::optim(c(meanlog=.9, sdlog=2.9), dlnorm_to_run, sims=sims)
best_par <- optimized_results$par
best_neglnL <- optimized_results$value
dented_results <- dent_walk(par=best_par, fn=dlnorm_to_run, best_neglnL=best_neglnL, sims=sims)
#> [1] "Calculating intervals at a confidence level of 95%"
#> [1] "Done replicate 50"
#> [1] "CI of values (the 23 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.9027427 2.615672
#> [2,] 394.8771 1.7154521 3.375664
#> [1] "Rough volume of good region is 0.617652654879225"
#> [1] "Done replicate 100"
#> [1] "CI of values (the 40 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.9027427 2.615672
#> [2,] 394.8771 1.7154521 3.375664
#> [1] "Rough volume of good region is 0.617652654879225"
#> [1] "Done replicate 150"
#> [1] "CI of values (the 65 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8982548 2.601432
#> [2,] 394.8771 1.7154521 3.375664
#> [1] "Rough volume of good region is 0.632699629330657"
#> [1] "Done replicate 200"
#> [1] "CI of values (the 91 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8982548 2.601432
#> [2,] 394.8771 1.8488812 3.375664
#> [1] "Rough volume of good region is 0.736004593627843"
#> [1] "Done replicate 250"
#> [1] "CI of values (the 105 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8982548 2.601432
#> [2,] 394.9361 2.1215997 3.400919
#> [1] "Rough volume of good region is 0.978047686083454"
#> [1] "Done replicate 300"
#> [1] "CI of values (the 133 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8982548 2.601432
#> [2,] 394.9361 2.1215997 3.579706
#> [1] "Rough volume of good region is 1.19676648386333"
#> [1] "Done replicate 350"
#> [1] "CI of values (the 158 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9361 2.1215997 3.579706
#> [1] "Rough volume of good region is 1.23983547805752"
#> [1] "Done replicate 400"
#> [1] "CI of values (the 182 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9361 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 450"
#> [1] "CI of values (the 203 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9361 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 500"
#> [1] "CI of values (the 212 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 550"
#> [1] "CI of values (the 221 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 600"
#> [1] "CI of values (the 239 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 650"
#> [1] "CI of values (the 247 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 700"
#> [1] "CI of values (the 270 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 750"
#> [1] "CI of values (the 291 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 800"
#> [1] "CI of values (the 309 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 850"
#> [1] "CI of values (the 328 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 900"
#> [1] "CI of values (the 344 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.7096698 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.45313834273627"
#> [1] "Done replicate 950"
#> [1] "CI of values (the 367 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.7096698 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.45313834273627"
#> [1] "Done replicate 1000"
#> [1] "CI of values (the 384 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.6517637 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.51273445015124"
plot(dented_results)
# Multivariate case
sims <- stats::rlnorm(100, meanlog=1, sdlog=3)
dlnorm_to_run <- function(par, sims) {
return(-sum(stats::dlnorm(sims, meanlog=par[1], sdlog=par[2], log=TRUE)))
}
optimized_results <- stats::optim(c(meanlog=.9, sdlog=2.9), dlnorm_to_run, sims=sims)
best_par <- optimized_results$par
best_neglnL <- optimized_results$value
dented_results <- dent_walk(par=best_par, fn=dlnorm_to_run, best_neglnL=best_neglnL, sims=sims)
#> [1] "Calculating intervals at a confidence level of 95%"
#> [1] "Done replicate 50"
#> [1] "CI of values (the 23 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.9027427 2.615672
#> [2,] 394.8771 1.7154521 3.375664
#> [1] "Rough volume of good region is 0.617652654879225"
#> [1] "Done replicate 100"
#> [1] "CI of values (the 40 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.9027427 2.615672
#> [2,] 394.8771 1.7154521 3.375664
#> [1] "Rough volume of good region is 0.617652654879225"
#> [1] "Done replicate 150"
#> [1] "CI of values (the 65 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8982548 2.601432
#> [2,] 394.8771 1.7154521 3.375664
#> [1] "Rough volume of good region is 0.632699629330657"
#> [1] "Done replicate 200"
#> [1] "CI of values (the 91 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8982548 2.601432
#> [2,] 394.8771 1.8488812 3.375664
#> [1] "Rough volume of good region is 0.736004593627843"
#> [1] "Done replicate 250"
#> [1] "CI of values (the 105 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8982548 2.601432
#> [2,] 394.9361 2.1215997 3.400919
#> [1] "Rough volume of good region is 0.978047686083454"
#> [1] "Done replicate 300"
#> [1] "CI of values (the 133 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8982548 2.601432
#> [2,] 394.9361 2.1215997 3.579706
#> [1] "Rough volume of good region is 1.19676648386333"
#> [1] "Done replicate 350"
#> [1] "CI of values (the 158 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9361 2.1215997 3.579706
#> [1] "Rough volume of good region is 1.23983547805752"
#> [1] "Done replicate 400"
#> [1] "CI of values (the 182 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9361 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 450"
#> [1] "CI of values (the 203 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9361 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 500"
#> [1] "CI of values (the 212 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 550"
#> [1] "CI of values (the 221 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 600"
#> [1] "CI of values (the 239 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 650"
#> [1] "CI of values (the 247 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 700"
#> [1] "CI of values (the 270 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 750"
#> [1] "CI of values (the 291 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 800"
#> [1] "CI of values (the 309 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 850"
#> [1] "CI of values (the 328 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.8542293 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.30435970658948"
#> [1] "Done replicate 900"
#> [1] "CI of values (the 344 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.7096698 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.45313834273627"
#> [1] "Done replicate 950"
#> [1] "CI of values (the 367 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.7096698 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.45313834273627"
#> [1] "Done replicate 1000"
#> [1] "CI of values (the 384 replicates within 2.99573227355399 neglnL of the optimum)"
#> neglnL meanlog sdlog
#> [1,] 391.9704 0.6517637 2.601432
#> [2,] 394.9386 2.1215997 3.630618
#> [1] "Rough volume of good region is 1.51273445015124"
plot(dented_results)